寻找新奇的量子物态，如拓扑绝缘体、反常量子霍尔效应、外尔半金属等，是近年来凝聚态物理和材料科学领域的研究热点。例如，拓扑绝缘体具有受拓扑保护的零能隙边界态，在无能耗传输、新型量子器件等方向上有广泛的应用前景。一般地，对于d维n阶的拓扑绝缘体而言，会在其（d-n）维的边界上出现边界态。但由于制造工艺等条件的限制，这些拓扑材料在实际应用方面面临严峻挑战。针对这一难题，利用集总参数电子线路中基尔霍夫方程与凝聚态物理紧束缚哈密顿量的对应关系，可以在传统的电子线路中设计出种类丰富的新型拓扑物态。此外，电路具有器件功能多样，制备工艺成熟、可靠等诸多优势，可以实现和验证传统凝聚态体系中难以实现或无法实现的物态（如非厄密拓扑态、高维拓扑态），为探索新奇量子物态及其实际应用提供了一个理想的平台。

近期，欧洲杯下单平台本科生姚俊杰在周苗教授的指导下，在拓扑电路的理论设计方面取得重要进展。通过理论计算，设计出一种类似凝聚态物理中凯库勒晶格的电路结构（图1），使电路的动力学特征矩阵具有与其哈密顿量一致的形式。有趣的是，可以通过调控电容值来实现拓扑相变，在电路意义下的能带里出现非零的四极矩，实现二维二阶拓扑绝缘体。相关研究成果以“Quadrupole topological phase and robust corner resonance in Kekulé hexagonal electric circuit”为题发表在专业物理领域的国际知名期刊New Journal of Physics上（论文链接：https://iopscience.iop.org/article/10.1088/1367-2630/abae88）。

图1设计的凯库勒六角电路结构

工作系统研究了一维半无限长电路和零维具有开放边界条件的有限大电路，在二者中分别发现了能隙非常小的边缘态和无能隙角落态，且该角落态的拓扑起源是非零的体四极矩，而不是由边缘偶极极化引起的瓦尼尔类角落态。同时，通过对体系电压分布的计算，发现电路的拓扑态能够通过外加输入的激励频率来灵活调控。当电路处于共振频率时，体系的两点电阻会在角落处出现一个极大的共振峰，为实验观察提供了一个极大的利好（图2）。在电路的实际应用时，不可避免地会出现器件参数的误差，该工作发现此电路对于一定程度内的误差具有良好的鲁棒性，拓扑态在该范围内不受影响，且电路的尺寸也可以做到很小而不导致拓扑态消失。这些发现对于未来拓扑电路实际研究和应用有重要的指导意义。

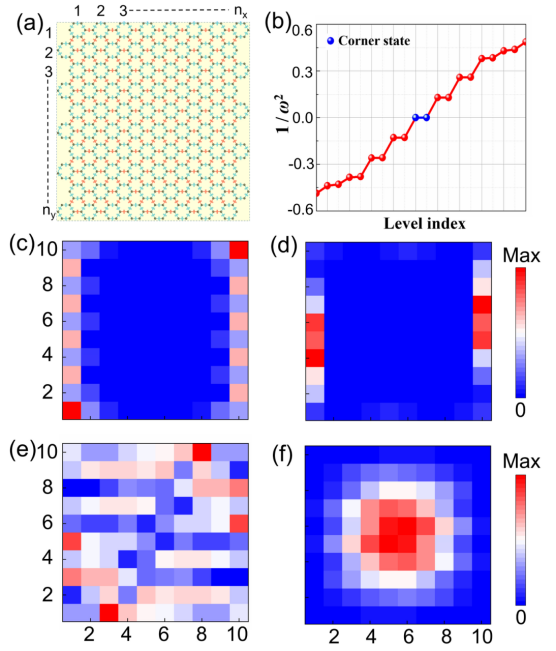
图2: (a) 0维电路示意图; (b)对应的能级分布; (c)-(f)不同激励频率下的电压分布

该论文的第一作者姚俊杰是欧洲杯下单平台2017级本科生。姚俊杰同学学习成绩优异，排名物理专业大班第1，获得包括国家励志奖学金（2018）、暑期社会实践校级二等奖及先进个人（2018）、北京市数学竞赛二等奖（2018），国家奖学金（2019），校级优秀生和学习优秀特等奖（2019），冯如杯科技竞赛二等奖（2020）等多个奖项及荣誉。姚俊杰积极参与科研活动，主要从事通过传统电路实现高维高阶拓扑态、自旋轨道耦合效应、冷原子系统等方向的理论研究。